Quando aprendemos a operar potências,
a primeira e mais simples regra que dominamos é que devemos sempre
multiplicar a base por ela mesma quantas vezes indicar o expoente. Por
exemplo, se temos a potência 210, devemos multiplicar o 2 por 10 vezes da seguinte forma:
210 = 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 1024
Mas e se o expoente for um número negativo? Como resolver a potência 2– 10? Vejamos uma nova regra que ajudará na resolução de potências com expoente menor do que zero!
Dada uma potência x – y, com x e y reais, o seu resultado é igual ao inverso de x elevado a y.
Para compreender essa definição,
precisamos primeiro compreender o que é o inverso de um número. Dado um
número qualquer, seu inverso é a fração cujo numerador é 1, e o denominador é o próprio número. Por exemplo, o inverso de 5 é  , e o inverso de 10 é
, e o inverso de 10 é  . Mas qual é o inverso de uma fração? A ideia é a mesma! Vejamos a fração ½: para encontrar seu inverso, vamos colocá-la como denominador de uma fração em que o numerador é 1 e fazer uma simples divisão de fração:
. Mas qual é o inverso de uma fração? A ideia é a mesma! Vejamos a fração ½: para encontrar seu inverso, vamos colocá-la como denominador de uma fração em que o numerador é 1 e fazer uma simples divisão de fração:
 , e o inverso de 10 é
, e o inverso de 10 é  . Mas qual é o inverso de uma fração? A ideia é a mesma! Vejamos a fração ½: para encontrar seu inverso, vamos colocá-la como denominador de uma fração em que o numerador é 1 e fazer uma simples divisão de fração:
. Mas qual é o inverso de uma fração? A ideia é a mesma! Vejamos a fração ½: para encontrar seu inverso, vamos colocá-la como denominador de uma fração em que o numerador é 1 e fazer uma simples divisão de fração:
Agora se você quiser simplificar mais ainda o processo para encontrar o inverso de uma fração, há uma dica infalível: basta inverter a fração, trocando o denominador de lugar com o numerador! Por exemplo, o inverso de 2/5 é 5/2, o inverso de 7/3 é 3/7 e o inverso de 1/4 é 4/1, ou, simplesmente, 4.
Voltando para a pergunta do início do texto, vamos calcular o valor de 2– 10.

Vejamos alguns outros exemplos de potências com expoente negativo e observe como esse assunto relaciona-se com a potenciação de números racionais:
1° Exemplo: 3 – 2
O inverso de 3 é 1/3. Logo, para calcular 3 – 2, faremos:

2° Exemplo: 10 – 1
O inverso de 10 é 1/10. Calculando 10 – 1, temos:

3° Exemplo: (3/4) – 3
O inverso de 3/4 é 4/3. Então (3/4) – 3 será dado da seguinte forma:

4° Exemplo: (– 2/3) – 4
O inverso de – 2/3 é – 3/2. Calculando (– 2/3) – 4, teremos:

Fração algébrica
É toda divisão de polinômios escrita na forma de fração cujo denominador apresenta, pelo menos, uma variável.Para Lembrar: fração é todo número racional escrito na forma
 , onde b ≠ 0.
, onde b ≠ 0.Observação: convencionando que o denominador de uma fração em R não pode ser zero, a partir daqui não serão mais indicadas as restrições para o denominador.
 → fração algébrica
→ fração algébrica → fração algébrica
→ fração algébrica![\frac{\sqrt[3]{8}}{2}](http://www.infoescola.com/wp-content/plugins/latex/cache/tex_94f2a47b193d2989cf5bed269ad4c5c7.gif) → fração não algébrica
→ fração não algébricaPotenciação de frações algébricas
Para calcular a potência de uma fração algébrica, elava-se o numerador e o denominador a potência dada.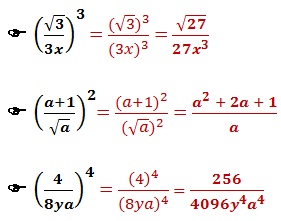
Quando se quer calcular a potência de um expoente negativo, inverte-se a fração inicial e eleva a fração invertida ao expoente positivo.
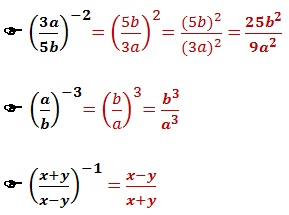
Para calcular a potência de potência de uma fração algébrica, conserva-se a fração e multiplica os expoentes entre si. Feito isso, eleva a potência ao novo expoente encontrado.
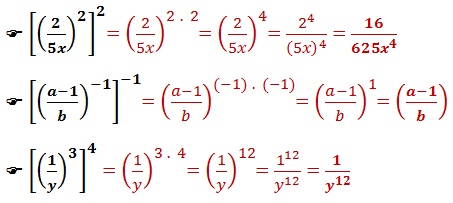
Atividades de fixação
1. Resolva as potências.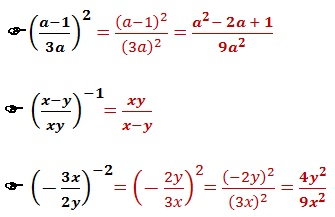
2. Calcule as potências de potências.
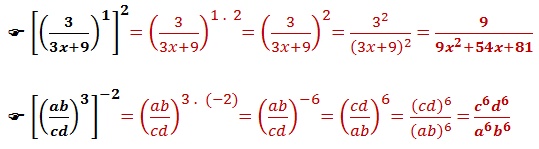

Nenhum comentário:
Postar um comentário